| Definitions | x(s),  T, state@i, Trans(T;x,y.E(x;y)), Sym(T;x,y.E(x;y)), Refl(T;x,y.E(x;y)), {T}, dt(l;da), case b of inl(x) => s(x) | inr(y) => t(y), suptype(S; T), x,y:A//B(x;y), T, state@i, Trans(T;x,y.E(x;y)), Sym(T;x,y.E(x;y)), Refl(T;x,y.E(x;y)), {T}, dt(l;da), case b of inl(x) => s(x) | inr(y) => t(y), suptype(S; T), x,y:A//B(x;y),   x,y. t(x;y), A x,y. t(x;y), A 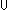 B, B,   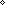 , EquivRel(T;x,y.E(x;y)), f , EquivRel(T;x,y.E(x;y)), f  g, s ~ t, eqof(d), if b then t else f fi , tt, ff, (x g, s ~ t, eqof(d), if b then t else f fi , tt, ff, (x  l), P l), P   Q, x Q, x  dom(f), strong-subtype(A;B), f(x), P dom(f), strong-subtype(A;B), f(x), P    Q, p Q, p   q, p q, p   q, p q, p    q, q,   b, deq-member(eq;x;L), a = b, a = b, qeq(r;s), q_less(a;b), q_le(r;s), eq_atom$n(x;y), [d] b, deq-member(eq;x;L), a = b, a = b, qeq(r;s), q_less(a;b), q_le(r;s), eq_atom$n(x;y), [d] , a < , a < b, x f y, a < b, x f y, a < b, null(as), x =a y, i b, null(as), x =a y, i  z j, i <z j, p =b q, a = b, inr x , inl x , es realizer ind Rrframe compseq tag def, only members of L read x, es realizer ind Rbframe compseq tag def, k sends only on links in L, es realizer ind Raframe compseq tag def, k affects only members of L, es realizer ind Rpre compseq tag def, (precondition a:Outcome(p) is P:State(ds) -> Bool), locl(a), Outcome, es realizer ind Rsends compseq tag def, with declarations ds:dsda:dak(v) sends f s v on link l, lnk-decl(l;dt), es realizer ind Reffect compseq tag def, with declarations ds:dsda:daeffect of k(v) is x := f s v, es realizer ind Rsframe compseq tag def, only L sends on (l with tg), <a, b>, es realizer ind Rframe compseq tag def, only members of L affect x :t, S z j, i <z j, p =b q, a = b, inr x , inl x , es realizer ind Rrframe compseq tag def, only members of L read x, es realizer ind Rbframe compseq tag def, k sends only on links in L, es realizer ind Raframe compseq tag def, k affects only members of L, es realizer ind Rpre compseq tag def, (precondition a:Outcome(p) is P:State(ds) -> Bool), locl(a), Outcome, es realizer ind Rsends compseq tag def, with declarations ds:dsda:dak(v) sends f s v on link l, lnk-decl(l;dt), es realizer ind Reffect compseq tag def, with declarations ds:dsda:daeffect of k(v) is x := f s v, es realizer ind Rsframe compseq tag def, only L sends on (l with tg), <a, b>, es realizer ind Rframe compseq tag def, only members of L affect x :t, S  T, es realizer ind Rinit compseq tag def, x : t initially x = v, Atom$n, es realizer ind Rplus compseq tag def, (i = T, es realizer ind Rinit compseq tag def, x : t initially x = v, Atom$n, es realizer ind Rplus compseq tag def, (i =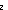 j), es realizer ind Rnone compseq tag def, M1 ||decl M2, , mk-ma, j), es realizer ind Rnone compseq tag def, M1 ||decl M2, , mk-ma,  , P & Q, State(ds), Valtype(da;k), t.1, f(x)?z, rcv(l,tg), t.2, EqDecider(T), IdLnkDeq, product-deq(A;B;a;b), True, , P & Q, State(ds), Valtype(da;k), t.1, f(x)?z, rcv(l,tg), t.2, EqDecider(T), IdLnkDeq, product-deq(A;B;a;b), True, 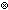 , f(a), IdDeq, Rds(R), KindDeq, Rda(R), p = q, R-base-domain(R), False, x : v, f , f(a), IdDeq, Rds(R), KindDeq, Rda(R), p = q, R-base-domain(R), False, x : v, f 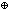 g, Top, g, Top, 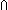 x:A.B(x), Void, Rnone(), #$n, left x:A.B(x), Void, Rnone(), #$n, left 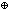 right, {x:A| B(x)} , Rinit(loc;T;x;v), Rframe(loc;T;x;L), Rsframe(lnk;tag;L), Reffect(loc;ds;knd;T;x;f), Rsends(ds;knd;T;l;dt;g), Rpre(loc;ds;a;p;P), Raframe(loc;k;L), Rbframe(loc;k;L), P right, {x:A| B(x)} , Rinit(loc;T;x;v), Rframe(loc;T;x;L), Rsframe(lnk;tag;L), Reffect(loc;ds;knd;T;x;f), Rsends(ds;knd;T;l;dt;g), Rpre(loc;ds;a;p;P), Raframe(loc;k;L), Rbframe(loc;k;L), P   Q, M1 || M2, R-base-ma(R), Rrframe(loc;x;L), Q, M1 || M2, R-base-ma(R), Rrframe(loc;x;L),  A, f || g, Realizer, rec(x.A(x)), A, f || g, Realizer, rec(x.A(x)), 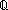 , ,  x.A(x), DeclaredType(ds;x), a:A fp x.A(x), DeclaredType(ds;x), a:A fp B(a), B(a),   x. t(x), FinProbSpace, State(ds), x. t(x), FinProbSpace, State(ds),  , Type, , Type,  x:A. B(x), x:A x:A. B(x), x:A  B(x), IdLnk, Id, Knd, type List, left + right, Unit, t B(x), IdLnk, Id, Knd, type List, left + right, Unit, t  T, T,  , s = t, x:A , s = t, x:A  B(x), B(x),  b b |
| Lemmas | Knd wf, Id wf, IdLnk wf, bool wf, decl-state wf, finite-prob-space wf, fpf wf, decl-type wf, rationals wf, unit wf, es realizer wf, fpf-compatible wf, not wf, assert wf, ma-compatible wf, R-base-ma wf, Rrframe wf, Rbframe wf, Raframe wf, Rpre wf, Rsends wf, Reffect wf, Rsframe wf, Rframe wf, Rinit wf, Rplus wf, Rnone wf, fpf-empty-compatible-right, top wf, fpf-empty wf, product-deq wf, idlnk-deq wf, Kind-deq wf, rcv wf, id-deq wf, pi2 wf, ma-state wf, true wf, fpf-single wf, fpf-empty-compatible-left, fpf-single wf3, false wf, member wf, fpf-join wf, ma-valtype wf, fpf-cap wf, lnk-decl wf, locl wf, p-outcome wf, fpf-compatible-singles-trivial, assert-eq-id, not functionality wrt iff, rev implies wf, iff wf, subtype rel wf, bnot wf, assert of bnot, iff transitivity, eqff to assert, eqtt to assert, eqof eq btrue, fpf-single-dom-sq, fpf-cap-single, fpf-join-cap-sq, equiv rel wf, b-union wf, int nzero wf, qeq wf2, quotient wf, btrue wf, subtype rel function, fpf-cap-single-join, fpf-compatible-singles, fpf-compatible-symmetry, eq id wf, pi1 wf, assert-eq-lnk, and functionality wrt iff, assert of band, eq lnk wf, band wf, assert-eq-knd, sym wf, trans wf, refl wf, int-rational, qeq wf, fpf-trivial-subtype-top, fpf-dom wf, ifthenelse wf, tunion wf, bfalse wf, squash wf, deq wf, eq knd wf, subtype rel product, subtype rel list |